tratamiento de datos y azar

viernes, 7 de enero de 2011

Distribucion normal

Una distribución de probabilidad ampliamente utilizada de una variable aleatoria discreta es la distribución binomial. Esta describe varios procesosde interés para los administradores.

Describe datos discretos, resultantes de un experimento denominado proceso de Bernoulli en honor del matemático suizo Jacob Bernoulli, quien vivió en el siglo XVII.

Empleo del proceso de Bernoulli.
Podemos servirnos de los resultados de un número fijo de lanzamientos de una moneda como ejemplo de un proceso de Bernoulli. Este proceso lo describimos así:

1. Cada ensayo ( cada lanzamiento, en nuestro caso) tiene sólo dos resultados posibles: lado A o lado B, sí o no, éxito o fracaso.

2.La probabilidad del resultado de cualquier ensayo (lanzamiento) permanece fija con el tiempo. Tratándose de una moneda la probabilidad de que salga de el lado A sigue siendo de 0.5 en cada lanzamiento, cualquiera que sea el número de veces que la moneda sea arrojada.

3. Los ensayosson estadísticamente independientes, es decir, el resultado de un lanzamiento no afecta al de cualquier otro lanzamiento.

Cada proceso de Bernoulli tiene su propia probabilidad característica. Pongamos el caso en que siete décimas partes de las personas que solicitaron cierto tipo de empleopasaron la prueba. Diremos entonces que la probabilidad característica fue de 0.7 pero podemos describir los resultados de la prueba como un proceso de Bernoulli sólo si tenemos la seguridad de que la proporción de los que fueron aprobados permaneció constante con el tiempo.

Des de luego, la otra característica del proceso de Bernoulli también deberá ser satisfecha. Cada prueba deberá arrojar tan sólo dos resultados (éxito o fracaso= y los resultados de las pruebas habrán de ser estadísticamente independientes.

En un lenguaje más formal, el símbolo p representa la probabilidad de un éxito y el símbolo q ( 1- p ) representa la probabilidad de un fracaso. Para representar cierto número de éxitos, utilizaremos el símbolo r y para simbolizar el número total de ensayos emplearemos el símbolo n.

Entonces tenemos que :

P	Probabilidad de éxito.
Q	Probabilidad de fracaso.
r	Número de éxitos deseados.
n	Número de ensayos efectuados.

Existe una fórmula binomial:
Probabilidad de r éxitos en n ensayos es :
N! / R! (N-R)! PR QN-R
Recordemos que el símbolo factorial! Significa por ejemplo que es 3! = 3*2*1 = 6

Los matemáticos definen 0! = 1.

3.3 DISTRIBUCION NORMAL
La Distribución Normal: una distribución de una variable aleatoria continua.

Una muy importante distribución continua de probabilidad es la distribución normal. Varios matemáticos intervinieron en su desarrolloentre ellos figura el astrónomo del siglo XVIII Karl Gauss, a veces es llamada en sus honor la distribución de Gauss.

Características de la distribución normal de la probabilidad.
1.La curva tiene un solo pico, por consiguiente es unimodal. Presenta una forma de campana.
2.La media de una población distribuida normalmente se encuentra en el centro de su curva normal.
3. A causa de la simetría de la distribución normal de probabilidad, la mediana y la moda de la distribución también se hallan en el centro, por tanto en una curva normal, la media, la mediana y la moda poseen el mismo valor.
4. Las dos colas (extremos) de una distribución normal de probabilidad se extienden de manera indefinida y nunca tocan el eje horizontal.
Áreas bajo la curva normal.
El área total bajo la curva normal será de 1.00 por lo cual podemos considerar que las áreas bajo la curva son probabilidades.
El valor de Z.
Z= Número de desviaciones estándar de x respecto a la media de esta distribución.
Z= x-m / s
X=valor de la variable aleatoria que nos interesa.
m = media de la distribución de esta variable aleatoria.
s = desviación estándar de esta distribución.

Las variables aleatorias distribuidas en forma normal asumen muchas unidades diferentes de medición, por lo que hablaremos de forma estándar y les daremos el símbolo de Z.

Ensayo de Bernoulli

En la teoría de probabilidad y estadística, un ensayo de Bernoulli es un experimento aleaorio en el que sólo se pueden obtener dos resultados (habitualmente etiquetados como éxito y fracaso). Se denomina así en honor a Jakob Bernoulli.
Desde el punto de vista de la teoría de la probabilidad, estos ensayos están modelados por una variable aleatoria que puede tomar sólo dos valores, 0 y 1. Habitualmente, se utiza el 1 para representar el éxito.
Si p es la probabilidad de éxito, entonces el valor del valor esperado de la variable aleatoria es p y su varianza, p (1-p).
Los procesos de Bernoulli son los que resultan de la repetición en el tiempo de ensayos de Bernoulli independientes pero idénticos.

Ejemplos

En la práctica, los ensayos de Bernoulli se utilizan para modelar fenómenos aleatorios que sólo tienen dos resultados posibles, como por ejemplo:

Al lanzar una moneda, comprobar si sale cara (éxito) o cruz (fracaso). Se suele suponer que una moneda tiene una probabilidad de éxito de 0,5.
Al lanzar un dado, ver si se obtiene un seis (éxito) o cualquier otro valor (fracaso).
Al realizar una encuesta política, tras escoger un votante al azar, ver si éste votará "si" en un referéndum próximo.
¿Era el recién nacido niña?
¿Son verdes los ojos de una persona?
¿Decidió un cliente potencial comprar determinado producto?

Hay que entender que éxito y fracaso son etiquetas para los resultados y que no debe ser interpretado literalmente.

Desviacion estandar

La desviación estándar o desviación típica (σ) es una medida de centralización o dispersión para variables de razón (ratio o cociente) y de intervalo, de gran utilidad en la estadística descriptiva.
Se define como la raíz cuadrada de la varianza. Junto con este valor, la desviación típica es una medida (cuadrática) que informa de la media de distancias que tienen los datos respecto de su media aritmética, expresada en las mismas unidades que la variable.
Para conocer con detalle un conjunto de datos, no basta con conocer las medidas de tendencia central, sino que necesitamos conocer también la desviación que representan los datos en su distribución respecto de la media aritmética de dicha distribución, con objeto de tener una visión de los mismos más acorde con la realidad al momento de describirlos e interpretarlos para la toma de decisiones.
Formulación
La varianza representa la media aritmética de las desviaciones con respecto a la media que son elevadas al cuadrado.
Si atendemos a la colección completa de datos (la población en su totalidad) obtenemos la varianza poblacional; y si por el contrario prestamos atención sólo a una muestra de la población, obtenemos en su lugar la varianza muestral. Las expresiones de estas medidas son las que aparecen a continuación.
Expresión de la varianza muestral:

${S_X^2} = \frac{ \sum\limits_{i=1}^n \left( X_i - \overline{X} \right) ^ 2 }{n}$

Segunda forma de calcular la varianza muestral:

${S_X^2} = \frac{ \sum\limits_{i=1}^n X_i^2}{n} - \overline{X}^2$

demostración

$\frac{ \sum\limits_{i=1}^n \left( X_i - \overline{X} \right) ^ 2 }{n} = \frac{ \sum\limits_{i=1}^n (X_i^2 + \overline{X}^2 -2X_i \overline{X})}{n} = \frac{ \sum\limits_{i=1}^n X_i^2 }{n} + \frac{ \sum\limits_{i=1}^n \overline{X}^2 }{n} - \frac{ \sum\limits_{i=1}^n 2X_i \overline{X}}{n} = \frac{ \sum\limits_{i=1}^n X_i^2 }{n} + \frac{ \overline{X}^2 \sum\limits_{i=1}^n 1 }{n} - \frac{ 2 \overline{X} \sum\limits_{i=1}^n X_i }{n}$

podemos observar que como

$\frac{ \sum\limits_{i=1}^n 1 }{n} = 1$ (sumamos n veces 1 y luego dividimos por n)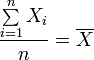

y como

$\frac{ \sum\limits_{i=1}^n X_i }{n} = \overline{X}$

obtenemos

$\frac{ \sum\limits_{i=1}^n X_i^2 }{n} + \overline{X}^2 - 2 \overline{X} \overline{X} = \frac{ \sum\limits_{i=1}^n X_i^2}{n} - \overline{X}^2$

Expresión de la cuasivarianza muestral (estimador insesgado de la varianza poblacional):

${S_X^2} = \frac{ \sum\limits_{i=1}^n \left( X_i - \overline{X} \right) ^ 2 }{n-1}$

Expresión de la varianza poblacional:

${\sigma^2} = \frac{ \sum\limits_{i=1}^N \left( X_i - {\mu} \right) ^ 2 }{N}$

donde

μ

es el valor medio de {

X i

}

Expresión de la desviación estándar poblacional:

$\sqrt{{\sigma^2}} =\sqrt{{\frac{ \sum\limits_{i=1}^N \left( X_i - {\mu} \right) ^ 2 }{N}}}$

El término desviación estándar fue incorporado a la estadística por Karl Pearson en 1894.
Por la formulación de la varianza podemos pasar a obtener la desviación estándar, tomando la raíz cuadrada positiva de la varianza. Así, si efectuamos la raíz de la varianza muestral, obtenemos la desviación típica muestral; y si por el contrario, efectuamos la raíz sobre la varianza poblacional, obtendremos la desviación típica poblacional.

Desviaciones estándar en una distribución normal.

Expresión de la desviación estándar muestral:

$\sqrt{s^2} =\sqrt{{ \frac{ \sum\limits_{i=1}^n \left( x_i - \overline{x} \right) ^ 2 }{n-1}}}$

También puede ser tomada como

$S = \sqrt{\frac{a-s^2/n}{n-1}}$

con a como $\sum_{i=1}^n x_i^2$ y s como $\sum_{i=1}^n x_i$ además se puede tener una mejor tendencia de medida al desarrollar las formulas indicadas pero se tiene que tener en cuenta la media, mediana y moda

Consideraciones sobre la hipótesis

Una hipótesis es una proposición aceptable que ha sido formulada a través de la recolección de información y datos, aunque no está confirmada sirve para responder de forma tentativa a un problema con base científica.

Una hipótesis puede usarse como una propuesta provisional que no se pretende demostrar estrictamente, o puede ser una predicción que debe ser verificada por el método científico. En el primer caso, el nivel de veracidad que se otorga a una hipótesis dependerá de la medida en que los datos empíricos apoyan lo afirmado en la hipótesis. Esto es lo que se conoce como contrastación empírica de la hipótesis o bien proceso de validación de la hipótesis. Este proceso puede realizarse mediante confirmación (para las hipótesis universales) o mediante verificación (para las hipótesis existenciales).

Pasos de la hipótesis

Los pasos de la hipótesis son reunir información, compararla, dar posibles explicaciones, escoger la explicación más probable y formular una o más hipótesis. Después de hacer todos estos pasos (en la ciencia) se realiza una experimentación, en la que se confirma la hipótesis o no. Si la hipótesis es confirmada, entonces lo planteado como hipotesis es verdadero. En caso de que no sea confirmada, la hipotesis es falsa.

Hipótesis de investigación

Una hipótesis de investigación representa un elemento fundamental en el proceso de investigación. Después de formular un problema, el investigador enuncia la hipótesis, que orientará el proceso y permitirá llegar a conclusiones concretas del proyecto que recién comienza.

Toda hipótesis constituye, un juicio o proposición, una afirmación o una negación de algo. Sin embargo, es un juicio de carácter especial. Las hipótesis son proposiciones provisionales y exploratorias y, por tanto, su valor de veracidad o falsedad depende críticamente de las pruebas empíricas disponibles. En este sentido, la replicabilidad de los resultados es fundamental para confirmar una hipótesis como solución de un problema.

La hipótesis de investigación es el elemento que condiciona el diseño de la investigación y responde provisionalmente al problema, verdadero motor de la investigación. Como se ha dicho esta hipótesis es una aseveración que puede validarse estadísticamente. Una hipótesis explícita es la guía de la investigación, puesto que establece los límites, enfoca el problema y ayuda a organizar el pensamiento.

Una hipótesis se considera explicación y por tanto toma cuerpo como elemento fundamental de una teoría científica, cuando el conocimiento existente en el área permite formular predicciones razonables acerca de la relación de dos o más elementos o variables.

Dicha hipótesis indica el tipo de relación que se espera encontrar:

Describe alguna o algunas propiedades de la relación entre A y B
El primer elemento A es la causa del segundo B
Cuando se presenta esto, A entonces sucede aquello, B.
Cuando esto sí, A, entonces aquello no, B.

Para que sea admitida como cuerpo de conocimiento científico, la hipótesis tiene que poder establecer una cuantificación determinada o una proporción matemática que permita su verificación estadística, pues el argumento meramente inductivo no es científicamente concluyente

USO DE LA ESTADISTICA

Al aplicar la estadística a un problema científico, industrial o social, se comienza con un proceso o población a ser estudiado. Esta puede ser la población de un país, de granos cristalizados en una roca o de bienes manufacturados por una fábrica en particular durante un periodo dado. También podría ser un proceso observado en varios instantes y los datos recogidos de esta manera constituyen una serie de tiempo.

Por razones prácticas, en lugar de compilar datos de una población entera, usualmente se estudia un subconjunto seleccionado de la población, llamado muestra. Datos acerca de la muestra son recogidos de manera observacional o experimental. Los datos son entonces analizados estadísticamente lo cual sigue dos propósitos: descripción e inferencia.

El concepto de correlación es particularmente valioso. Análisis estadísticos de un conjunto de datos puede revelar que dos variables (esto es, dos propiedades de la población bajo consideración) tienden a variar conjuntamente, como si hubiera una conexión entre ellas. Por ejemplo, un estudio del ingreso anual y la edad de muerte podría resultar en que personas pobres tienden a tener vidas más cortas que personas de mayor ingreso. Las dos variables se dicen que están correlacionadas. Sin embargo, no se puede inferir inmediatamente la existencia de una relación de causalidad entre las dos variables. El fenómeno correlacionado podría ser la causa de una tercera, previamente no considerada, llamada variable confusa.

Si la muestra es representativa de la población, inferencias y conclusiones hechas en la muestra pueden ser extendidas a la población completa. Un problema mayor es el de determinar que tan representativa es la muestra extraída. La estadística ofrece medidas para estimar y corregir por aleatoriedad en la muestra y en el proceso de recolección de los datos, así como métodos para diseñar experimentos robustos como primera medida, ver diseño experimental.

El concepto matemático fundamental empleado para entender la aleatoriedad es el de probabilidad. La estadística matemática (también llamada teoría estadística) es la rama de las matemáticas aplicadas que usa la teoría de probabilidades y el análisis matemático para examinar las bases teóricas de la estadística.

El uso de cualquier método estadístico es válido solo cuando el sistema o población bajo consideración satisface los supuestos matemáticos del método. El mal uso de la estadística puede producir serios errores en la descripción e interpretación, afectando las políticas sociales, la práctica médica y la calidad de estructuras tales como puentes y plantas de reacción nuclear.

Incluso cuando la estadística es correctamente aplicada, los resultados pueden ser difícilmente interpretados por un inexperto. Por ejemplo, el significado estadístico de una tendencia en los datos, que mide el grado al cual la tendencia puede ser causada por una variación aleatoria en la muestra, puede no estar de acuerdo con el sentido intuitivo. El conjunto de habilidades estadísticas básicas (y el escepticismo) que una persona necesita para manejar información en el día a día se refiere como «cultura estadística».